La prospettiva nel rinascimento

Dopo gli studi empirici di Brunelleschi e Masaccio, Leon Battista Alberti pubblica il De Pictura che contiene una prima descrizione sull'idea di prospettiva. In questo trattato però l'opera di Alberti è ancora legata ad un certo empirismo che ci danno dei risultati approssimati. Le varie scuole d’arte tenevano segreti i metodi adottati, spesso trasmessi  oralmente dal maestro. Uno di questi metodi è il così detto metodo delle superbipartienti che indica la diminuzione delle distanze man mano che ci avviciniamo verso il punto centrico sull'orizzonte. Le piastrelle di un pavimento rappresentate in prospettiva appaiono più piccole di un terzo verso il punto centrico , come la proporzione che passa tra 9, 6 o tra 6 e 4. Il metodo consiste nel dividere in direzione del punto centrico le distanze nella proporzione superbipartiente, cioè diminuendo via via di un terzo la quantità trovata. Il risultato ad occhio si avvicina alla realtà, ma non è esatto. Un altro metodo, per realizzare lo scorcio di una pavimentazione regolare, ci viene descritto da Ignazio Danti (Le due regole della prospettiva pratica anno 1583). In effetti quello che descrive il Danti è un metodo empirico, evidentemente in uso a quei tempi, che non ha nulla a che fare con la prospettiva. Questo problema viene superato da Piero della Fancesca che a Urbino alternando studi di matematica e arte, compone nel 1475 il De prospectiva Pingenti, opera in cui per la prima volta si affronta il problema della prospettiva con la matematica.

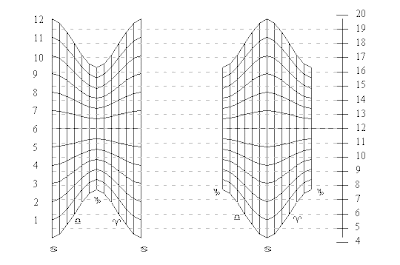
A sbloccare questa situazione di stallo è stato un allievo di Federico Commandino, Guidobaldo del Monte, il cui trattato Prospectivae libri Sex, pubblicato a Pesaro nel 1600, inizia ad affrontare l'argomento con spirito scientifico. Guidobaldo prende in considerazione e conferma il lavoro scientifico fatto da Commandino sul planisfero di Tolomeo. Fu infatti Commandino a fissare il rapporto tra planisfero e prospettiva. Il planisfero di Tolomeo trasporta i cerchi più significativi sul piano dell'equatore fissando il punto centrico sul polo australe. I cerchi dei paralleli di declinazione del sole, proiettati sul piano dell'equatore si ricostruiscono sull'equatore in altrettanti cerchi, mentre i meridiani si trasformano in rette. I cerchi posti sotto il piano equatoriale, più vicini al centro di proiezione, trasportati sull'equatore appaiono più grandi, mentre quelli sopra l'equatore, più lontani dal centro di proiezione, appaiono più piccoli. Disegnati i cerchi significativi sul piano equatoriale, un osservatore ponendo l'occhio al centro del piano equatoriale alla distanza uguale al raggio, vede la sfera in prospettiva con vista dal polo australe.  Guidobaldo proietta la sfera, spostando il centro di proiezione nel punto dove l'eclittica intercetta l'equatore, condizione che ruota il piano di proiezione, perpendicolare all'equatore, senza cambiare il metodo della proiezione. Si comincia a studiare la prospettiva ricorrendo ai trattati di Euclide e Tolomeo, confermando che a quei tempi, lo stesso problema, si era gia affrontato  con la geometria e l'ottica.